Decision Trees

2021-01-18 22:51:55 # decision trees # random forest

Decision Trees là một trong những thuật toán phổ biến trong Machine Learning, là tiền đề để phát triển các thuật toán phức tạp hơn như Random Forest, XGBoost và LightGBM. Hôm nay mình sẽ cùng nhau tìm hiểu thuật toán này nhé.

Random Forests meme

Bài toán thực tế

Phân loại hoa với tập dữ liệu iris

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split

# load dữ liệu iris
iris = load_iris()

# tách features (X) và label (y)
X = iris.data[:, 2:]
y = iris.target

# chia dữ liệu thành 2 tập train và test, với tỷ lệ 
# tập test là 0.2
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42)

# xây dựng model
clf = DecisionTreeClassifier(max_depth=2)
# train model
clf.fit(X_train, y_train)

# dự đoán trên tập test
y_pred = clf.predict(X_test)

# đánh giá kết quả dựa trên accuracy score
print("[INFO] accuracy score: ", accuracy_score(y_test, y_pred))

Dự đoán giá nhà với tập dữ liêu boston

from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split

# load dữ liệu boston
boston = load_boston()

# tách features (X) và label (y)
X = boston.data
y = boston.target

# chia dữ liệu thành 2 tập train và test, với tỷ lệ 
# tập test là 0.2
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42)

# xây dựng model
clf = DecisionTreeRegressor(max_depth=2)
# train model
clf.fit(X_train, y_train)

# dự đoán trên tập test
y_pred = clf.predict(X_test)

# đánh giá kết quả dựa trên r2_score
print("[INFO] r2_score: ", r2_score(y_test, y_pred))

Ý tưởng thuật toán

Hiểu đơn giản là thuật toán xây dựng một cây quyết định, liên tục phân chia tập dữ liệu về các nhánh. Thuật toán này có thể dùng cho cả bài toán phân loại (classification) và hồi quy (regression).

Có nhiều phương pháp implement thuật toán Decision Trees, ví dụ như ID3, C4.5, C5.0 và CART. Thư viện sklearn sử dụng phiên bản tối ưu của CART.

Phân loại

Trở lại bài toán phân loại hoa, sử dụng đoạn code dưới đây để xem cây quyết định trông thế nào nhé.

from sklearn.tree import export_graphviz
import graphviz
import matplotlib as plt

dot_data = export_graphviz(
            clf,
            out_file=None,
            feature_names=iris.feature_names,
            class_names=iris.target_names,
            rounded=True,
            filled=True,
            special_characters=True
        )

graph = graphviz.Source(dot_data)
# lưu graph ra file graph.png
graph.render("iris-tree", format="png")
# hiển thị graph
graph

Và bing-go, cây sẽ như này nè:

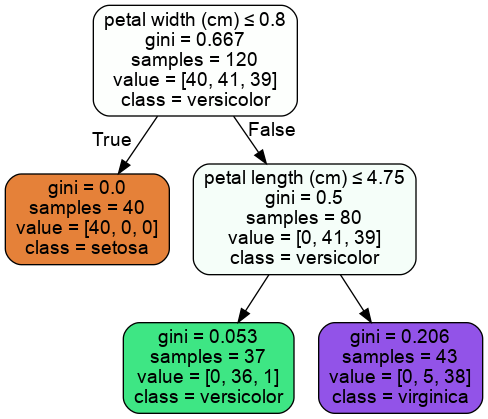
iris tree

Giải thích cây quyết định:

Bắt đầu từ node trên cùng (hay node root), với điều kiện $petal\ width \leq 0.8$, dữ liệu nào thỏa mãn điều kiện sẽ đi về nhánh trái, còn lại sẽ đi về nhánh phải. Node màu cam không có nhánh con nào nên được gọi là node lá, và dữ liệu ở node này sẽ được kết luận luôn là thuộc class setosa. Node màu xám (có nhánh con nên được gọi là node phân chia hay splitting node) tiếp tục phân chia tập dữ liệu thuộc node này về 2 node xanh và tím dựa trên điều kiện $petal\ length \leq 4.75$
Một số thông tin khác của node bao gồm:
- gini: mô tả “độ thuần khiết” (impurity) của node, dao động từ 0 đến 1. Trong đó 0 nghĩa là tất cả dữ liệu thuộc cùng 1 class, nên chúng ta luôn muốn gini nhỏ nhất có thể
  
  Công thức tính gini cho node $i$ như sau: $G_i = 1-\sum_{k=1}^{n}p_{i,k}^2$
  
  Trong đó:
  - $p_{i,k}$ là tỉ lệ số phần tử của class k trên tổng số samples.
    
    Ví dụ: ở node màu tím, $G=1-(0/43)^2-(5/43)^2-(38/43)^2\approx0.206$
- samples: số lượng dữ liệu training thuộc node
- value: số lượng dữ liệu của từng class trong node, ví dụ node tím có 0 setosa, 5 versicolor và 38 virginica

Hồi quy

Cây quyết định cho bài toán dự đoán giá nhà như sau:

from sklearn.tree import export_graphviz
import graphviz
import matplotlib as plt

dot_data = export_graphviz(
            clf,
            out_file=None,
            feature_names=boston.feature_names,
            rounded=True,
            filled=True,
            special_characters=True
        )

graph = graphviz.Source(dot_data)
# lưu graph ra file graph.png
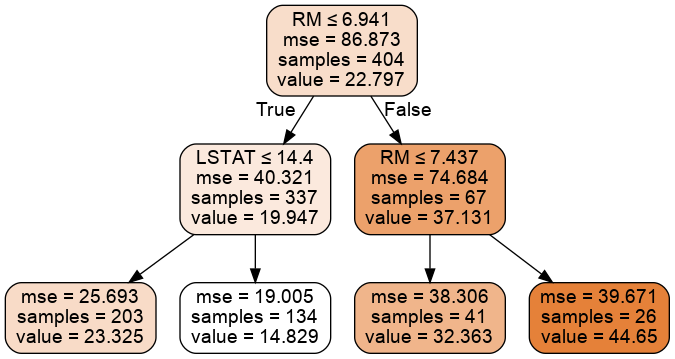
graph.render("boston-tree", format="png")
# hiển thị graph
graph

boston tree

Cây quyết định cho bài toán hồi quy khá giống với phân loại, ngoại trừ:

gini được thay bằng MSE

Công thức tính MSE cho node $i$ như sau: $MSE_i = \sum_{i\in node}(y_i - \bar{y})^2$

Trong đó:
- $y_i$ là label của từng phần tử trong node
- $\bar{y} = \frac{1}{tổng\ số \ phần\ tử\ của\ node}\sum_{i\in node}y_i$
dự đoán value, thay vì class

Phương pháp CART

Bước 1: chia tập dữ liệu thành 2 tập con sử dụng feature $k$ và giá trị $t_k$, sao cho hàm cost dưới đây là nhỏ nhất
$J(k,t_k)=\frac{m_{trái}}{m}G_{trái}+\frac{m_{phải}}{m}G_{phải}$

Trong đó:
- $m_{trái}$ và $m_{phải}$ là số lượng dữ liệu của 2 node trái và phải (2 tập con)
- $m$ là số lượng dữ liệu ở node hiện tại
- $G_{trái}$ và $G_{phải}$ là gini của 2 node trái và phải
Bước 2: tiếp tục phân chia các tập con sử dụng logic tương tự bước trên, cho tới khi thỏa mãn điều kiện dừng, ví dụ như:
- đạt độ sâu tối đa (quy định bởi hyperparameter max_depth)
- không thể phân chia sao cho gini của các tập con nhỏ hơn tập gốc

Tài liệu tham khảo

[1] Aurlien Gron. 2020. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems (2nd. ed.). O’Reilly Media, Inc.
[2] Brownlee, J. (2016) Machine Learning Mastery with Python. Machine Learning Mastery, EBook.
[3] https://towardsdatascience.com/decision-trees-in-machine-learning-641b9c4e8052

2021-01-18 22:51:55 # decision trees # random forest